はじめに
僕は心底うんざりしています。
大学生活も後半戦を迎え、試しに就活とやらをやってみてはいるのですが、そのあまりのしょーもなさに飽き飽きしているんです。
僕らはいつまで受験の真似事を繰り返すのでしょうか。
どこに行っても「あのSPIの答え俺持ってるわ〜」とか「俺外資必勝講座取ってるんだけど〜」とか「私、あの○○商社の××さんと知り合いなんだよね〜」とか、本当にしょうもない話をしてるんですよ。もうそんなのにはうんざりなんです。
受験の時もそうです。高校受験の時、塾に行かず家で一人で勉強していた僕は、冬休みの二週間だけ塾に通ったんですが、不健康そうな牛乳瓶の底みたいなメガネをかけたモヤシや巨漢に囲まれ、こいつらは勉強してるだけなのか、外で野球とかしないのかと愕然としたのを覚えています。

同じく浪人して通った予備校も勉強に命をかけてきたような同世代に囲まれ、彼らのどうでもいい模試自慢を聞かされて心底受験が嫌になりました。
そしてシューカツとやらでもまたそれなんです。受験のごとくいい会社に入るためにテクニックやコネやらをこねくり回す人たちに囲まて、僕は心底嫌な気分になりました。またこんなことをするのかと。お前らはいつまで自分の評価を他人に委ねて生きるんだと。とはいえ僕もそのレールにちょっと乗ろうとしているので偉そうなことは何も言えないんですがね。
そんなわけでテストやら面接やらを受けていると、こんなことを話しているのが聞こえました。
「お前、フェルミ推定やった?」
「当たり前じゃん。あれできなきゃ詰むわ」
出た。フェルミ推定。僕も何度かその名前は聞いたことがあります。意識の高そうな文系が何かと口にする「東京にあるマンホールの数は?」とか「バスにゴルフボールはいくつ詰められる?」とかそんなのわかるわけねえだろアホかとキレたくなるようなものを推定させる問題です。
その会話がちらっと聞こえた僕は試しに日本のマンホールの数を推定してみたのですが、ちっとも分かりません。あれ、難しくね?日本の人口を1億3000万人として、1世帯が3人として、一家に一個トイレがあって、トイレの数だけマンホールがあるとして、あれ、でも学校とかオフィスビルとかあるよな?あれ、これどうやるんだ?
ガーン。あんなにバカにしていたのにいざやれとなると全く分からない。ちくしょー。一応理系の僕は珍しく悔しくなりました。という訳で書店で良さげな本を手に取り、フェルミ推定についてちょっと勉強してみました。
1. フェルミ推定とは
今回参考にしたのはこちらの本。

この本によるとフェルミ推定とは「直感では見当のつかないような荒唐無稽な数量を、知っている知識だけをもとに、合理的な仮定とロジックを駆使して、短時間で概算する方法」を指しているらしいです。
そんでもって基本体系が下の図のようになるとのこと。
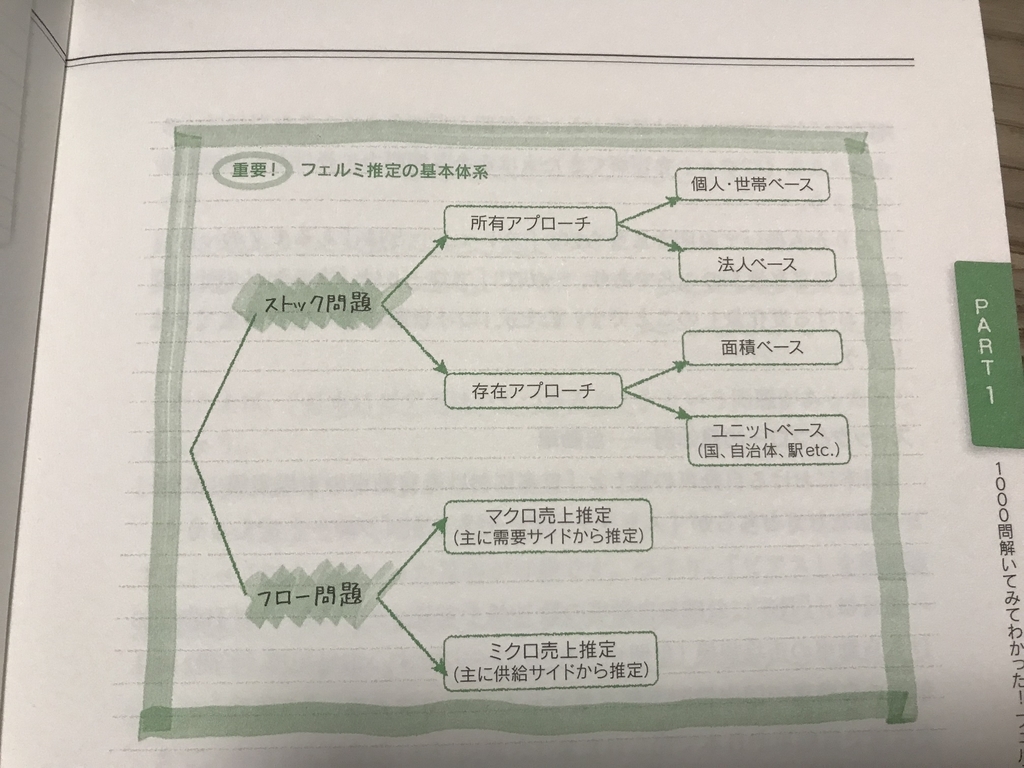
でもってフェルミ推定は
①「あるモノの一時点のの存在量」を表すストック問題
②「あるモノの一定期間における変化量」を表すフロー問題
の2つに分けられます。例えば「日本の自動車の数」はストック問題で、「日本の年間の自動車の市場規模」はフロー問題って感じで。
でストック問題へのアプローチとして、モノを持ってる人主体で考える「所有アプローチ」と、モノが存在する空間で考える「存在アプローチ」の二種類があります。
例えば「ピアスの数はいくつ」と聞かれたら「若い女性がつけてるよなあ」→所有アプローチ、「電柱の数はいくつ」と聞かれたら「家の周りにいくつあったっけ?」→存在アプローチってな具合で。
そんでもう一個のフロー問題については「マクロ売り上げ推定」と「ミクロ売り上げ推定」の2つがあって、
①マクロ売り上げ推定=市場規模確定→需要サイドから考える
②ミクロ売り上げ推定=一店舗ないし複数店舗の売り上げ推定→供給サイドから考える
なんだそう。まだついていけます。
では実際のフェルミ推定の流れを確認してみましょう。
2. フェルミ推定の流れ
フェルミ推定は
(i)前提確認
(ii)アプローチ設定
(iii)モデル化
(iv)計算実行
(v)現実性検証
の流れで進めていきます。言葉の説明は面倒なので実際にこの本にあったミネラルウォーターの「ボルビック」の日本の年間消費量を求めてみましょう。

(i)前提確認
まずボルビックを
①持ち歩ける500ml以下のペットボトルと
②持ち歩けない500mlより大きいペットボトル
に分けます。
その理由は持ち運びできるか否かで消費量が違うと予想したからです。
で①は300mlの小ボトルと500mlの大ボトルの二種類。
②は1000mlの小ボトルと1500mlの大ボトルがある。
でもって①は個人ベースで、②は世帯ベースで計算しますよと。こんな感じでこれから俺はこうやって考えるぞーってのを整理するのが前提確認です。
(ii)アプローチ設定
続いてアプローチを確認します。
①のボルビックの消費量は
A:日本の人口×B:ミネラルウォーターの平均消費本数×C:ボルビック選択率(シェア)×D:ボルビックの平均容量
で求められますってな具合で。でこの
A:日本の人口=1億2000万
C:ボルビック選択率(シェア)=20%
D:ボルビックの平均容量=(300ml+500ml)÷2=400ml
とすると仮定します。このCの選択率は自分の経験で仮定することになります。コンビニでミネラルウォーターの棚を見たらボルビックが2割くらいだった気がするとか。ここは完全に普段の観察力が試されるところです。
(iii)モデル化
ただこれだと大雑把すぎるので、さらに細かく分けて考えます。
ではここでミネラルウォータの消費本数を求めてみましょう。
例えばこんな感じで世代別、性別で消費量を考えるんです。これは1ヶ月の消費量の表です。

これも自分の頭で推測して数を決めます。例えば20歳未満は清涼飲料水を好むからあんまミネラルウォーター飲まなそうとか、男性より女性の方が飲みそうとかね。
でもって人口1億2000万をここでは0歳から80歳までに単純化して、各世代男女が同数で人口も同じと仮定します。その結果各世代の男女は
1億2000万人÷8÷2=750万人
になるわけです。
こんな感じで細かくさっきの数式を縦に分解していくのがモデル化です。
(iv)計算実行
さて、今までの過程をもとに計算します。すると
750万人×94本×12ヶ月≒750万×100本×12ヶ月=90億本になります。
でこいつを最初の式にぶち込んで...
90億本×20%×400ml=7200億ml=7.2億L
と求められたわけす。なるほどね!
(v)現実性検証
で最後に大事なのが出てきた数値の検証です。この計算の結果、90億本×20%÷1億2000万=15本、日本人は一人当たり1年間でボルビックのミネラルウォーターを飲んでいるとなりました。しかしさっきはエビアンやクリスタルガイザーに対するシェアを考えましたが、実際には国産のミネラルウォーターもあるのでもう少し本数は少なくなるはずなんです。
つまり正確に言えば
輸入ミネラルウォーターのシェア×ボルビックのシェア20%
となるので20本よりは少なくなるでしょうという具合です。
この最後の現実性の検証を忘れないようにしましょう。
こんな具合で個人の消費量を求めた後は続いて世帯ベースの値を求めるわけですが、こちらも日本の平均世帯人数を3人と過程したりして世帯数を求め、同様に計算していきます。
ただこの場合も落とし穴があり、個人と世帯の消費量を求めましたが、ミネラルウォーターを買うのは個人や世帯のみならず、会社などの法人もあるわけです。こういった点も見逃さず前提にもれなく組み込むことで良い推定ができるってわけです。実際にやってみてください。
3. いろんなフェルミ推定
フェルミ推定は基本的に先ほどの手順を応用して値を算出することができます。他にも
日本にあるぬいぐるみの数は?
ゴミ箱の数は?自動車の数は?ポストの数は?
スタバの売り上げは?カラオケの売り上げは?
などなどなんにでも使うことができます。確かにめちゃめちゃ頭の体操になりますな。
ちなみに冒頭で紹介した東京にあるマンホールの数は?って問題はこんな感じになるそうです。
もちろんこの値じゃないとダメ!っていう訳ではありません。フェルミ推定で大切なのは値の正確さではなく、どうしてその仮定を用いたかという根拠と論理性です。必要な選択肢を網羅し、理由を持って取捨選択し、素早く計算することが求められます。
フェルミ推定なんて無駄にかっこいい名前が付いていていかにもシューカツっぽいカッコつけだと思ってましたが、要はどこまで自分の頭で論理的に考えて推測できるかってところが大切なわけです。
やってみると結構面白いので、ぜひ皆さんもやってみてください。
はあ。クリスマスなのになんて記事を書いてるんだ俺は......