今日も研究が進まなかった、会社で上司にこっぴどく叱られた、恋人にフラれた...そんなとき、ふっと駅のホームに引き込まれ、危うく電車に...なんて経験があるかもしれません。
駅のホームは常に死と隣り合わせです。僕は日常でこんなに死ぬ可能性が高い場所があっていいのかと思ってます。足を滑らせば、誰かがちょっと体を押せば、電車に巻き込まれて木っ端微塵になってしまうんです。めちゃめちゃおっかないです。早く全ての駅にホームドアを設置してほしいものだといつも思ってます。
さて前置きはここまでにして、なぜ電車が通過するとホームに引き込まれるのか、簡単に説明しようと思います。
ここで用いるのが、このベルヌーイの定理ってものです。
(僕は数式を自作するすべを知らないので手書きで失礼します。)
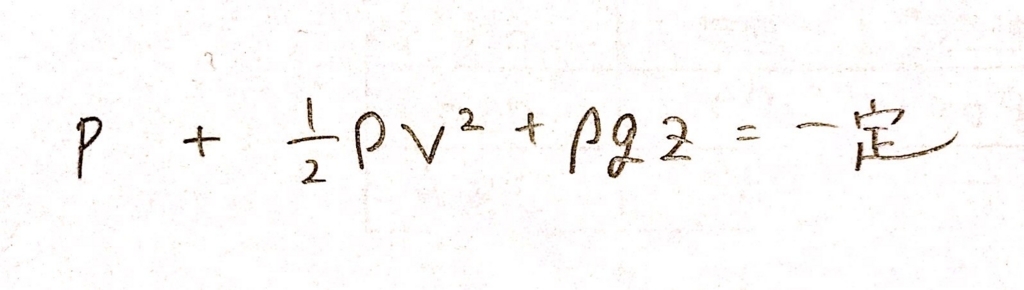
Pは圧力、ρは密度、Vは速度、gは重力加速度、zは位置を表します。
例えば野球のカーブが曲がる原理がこれで説明できます。
下の図のように回転するボールがあるとします。
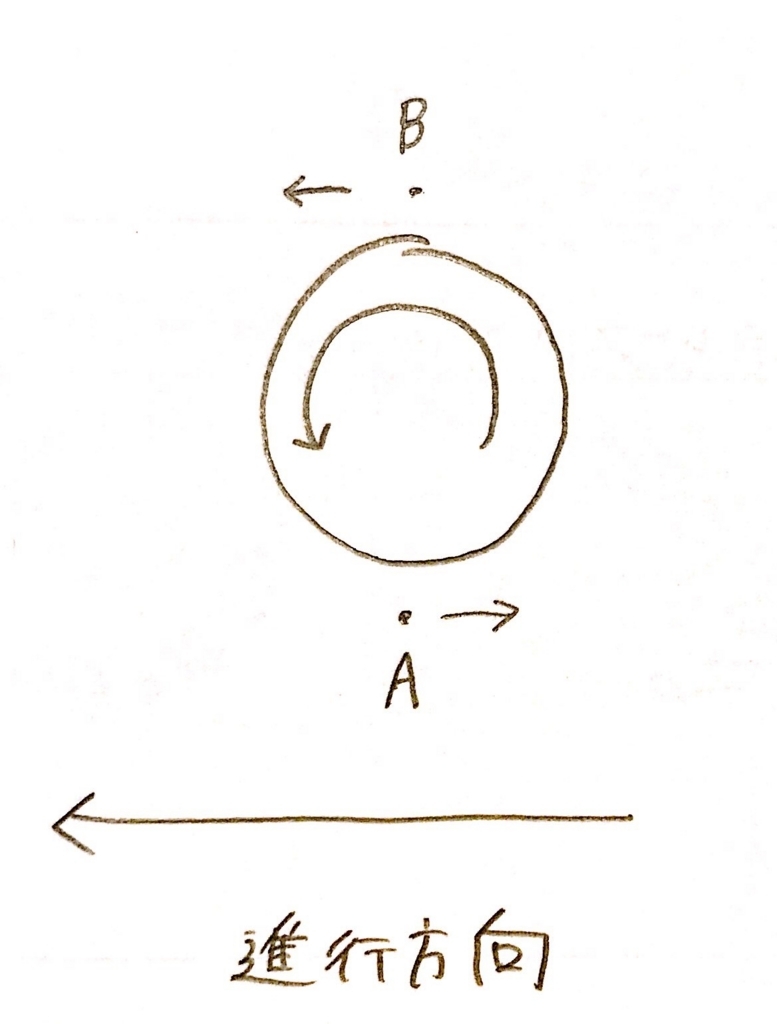
この時、ボールの下側A点の空気の流れは、上側のB点より速いです。
つまりA点では速度Vが大きくなります。
でもベルヌーイの定理にあるように、Vが大きくなっても他の項を足したら同じ値、一定値にならなくちゃいけないんですよね。
だから速度Vが大きくなると、代わりに圧力Pが小さくなります。
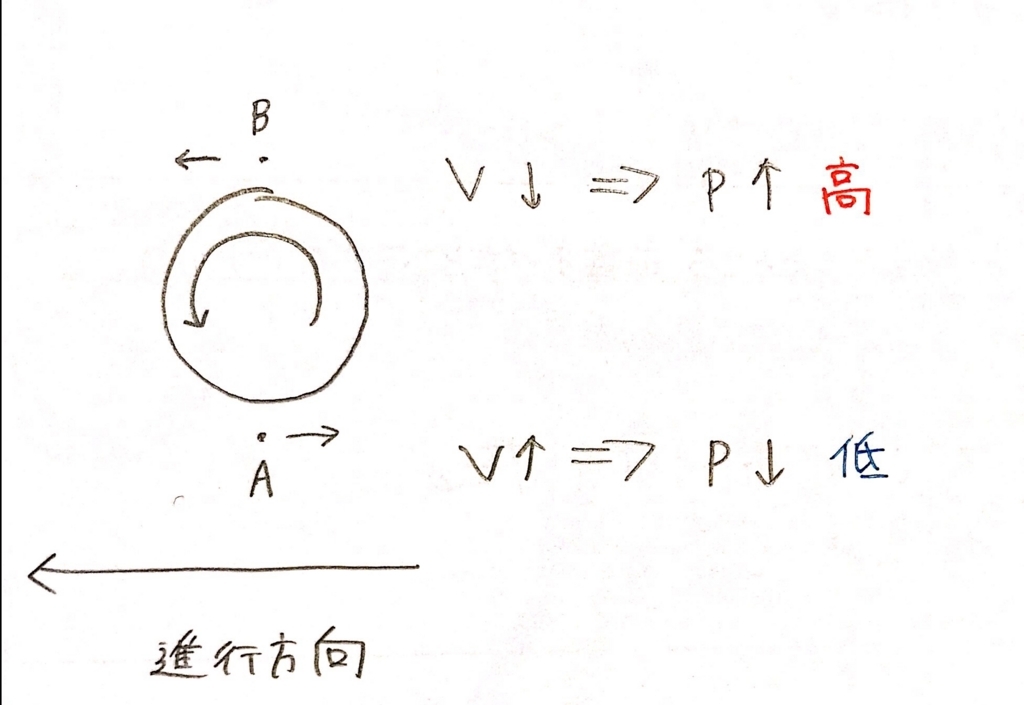
(ベルヌーイの定理にあったzはここでは高さの違いを表すんですけど、ボールは数センチほどなのでこの違いは無視できます。あとρは密度なので変化しません。)
反対に、上側B点はVが小さくなったので、代わりにPが大きくなります。つまり、下側A点の圧力より、上側B点の圧力の方が大きくなるわけです。そして圧力Pが大きい方から小さい方に力が働くので、結果としてボールは下向きに力を受けます。
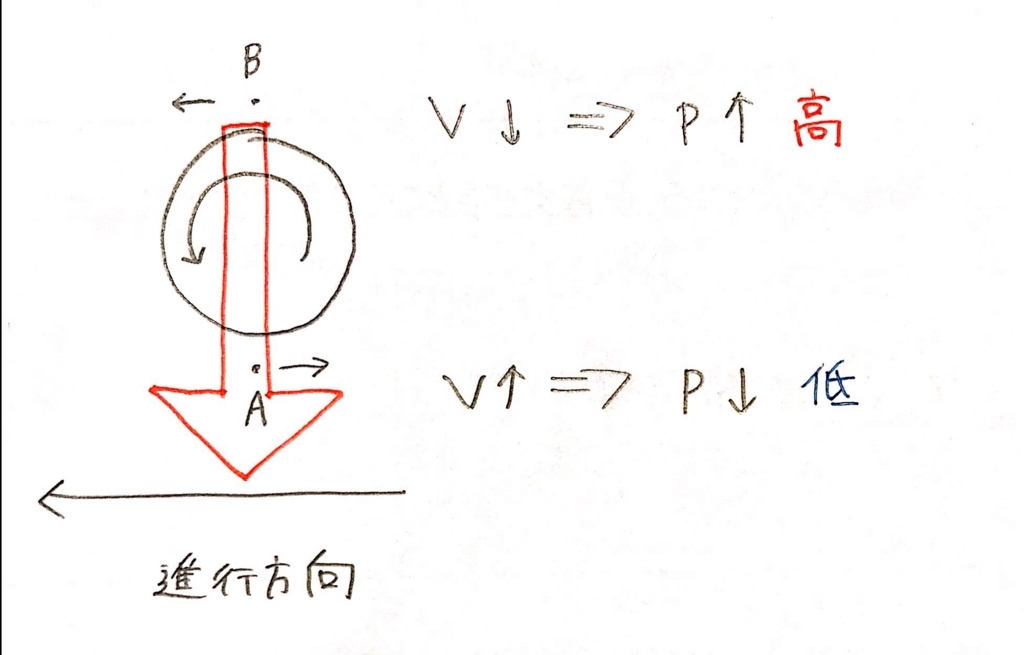
だからボールが落ちるんです。
ちなみにこの効果をマグヌス効果って言います。
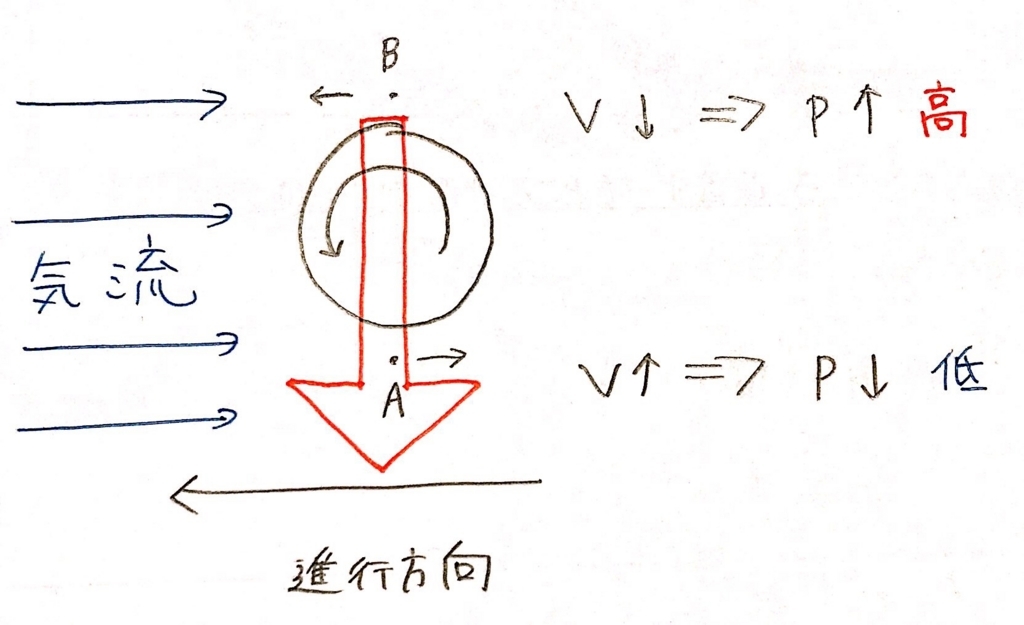
なんで下側のAの方が空気の流れが速いのー?って人は気流を考えてみてください。今ボールが矢印の方向に進んでるってことは、こんな風に気流がぶつかってくるってことですよね。今、ボールの下側は気流と同じ向きに動いてますから、この足し算で速くなるわけです。逆に上側B点は反対の向きなので引き算で遅くなります。
でもほんとはカーブって落ちるだけじゃなくて曲がるんですよね、その曲がる理由もこれと似たようなものなのでここでは割愛します。
あといいピッチャーが投げる浮き上がるストレートってのもこれで説明できます。今のカーブはトップスピンっていう回転をしてますが、ストレートはそれと反対方向のバックスピンです。つまりさっきと反対の上向きに力が働くわけです。
ボールの回転数が多いほど、空気の流れが速くなり、より大きな圧力差が生まれ働く力が大きくなります。だから回転数って大切なんですよね。
これでだいたいベルヌーイの定理が掴めたでしょうか。
さあ本題の電車についてですが、ここまでくればもう簡単です。
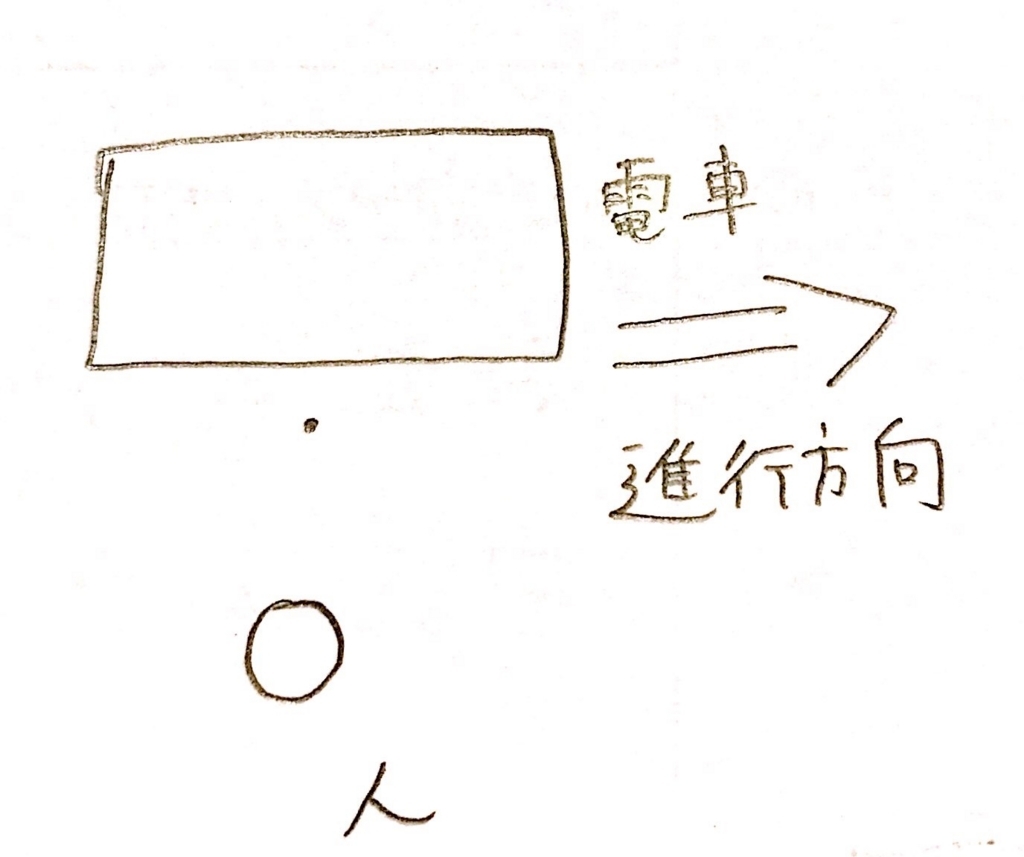
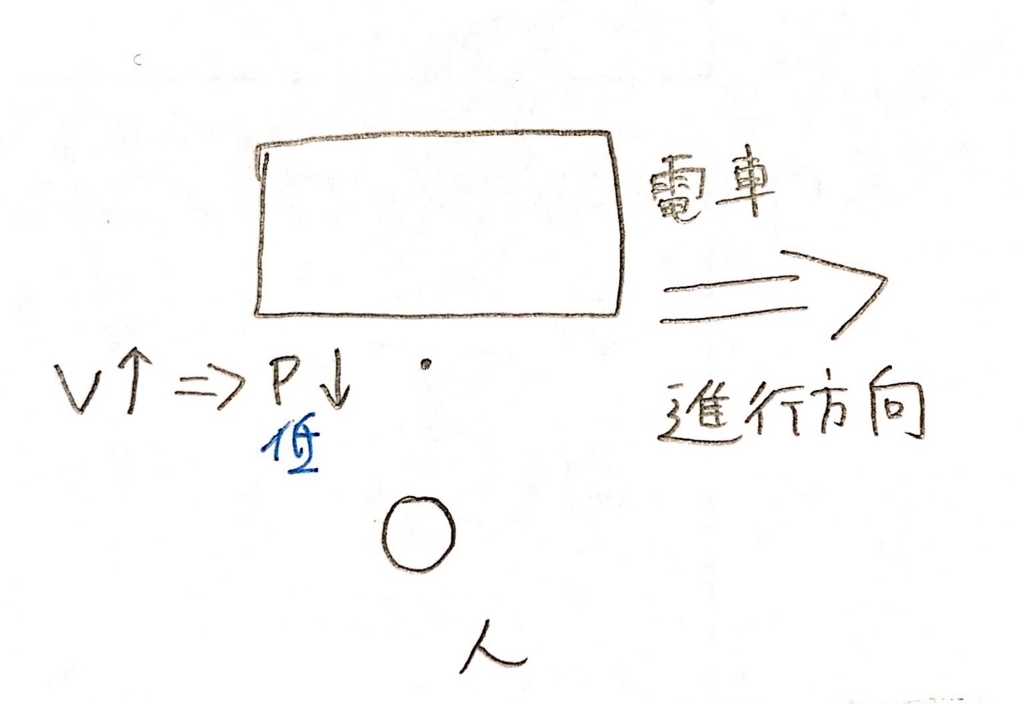
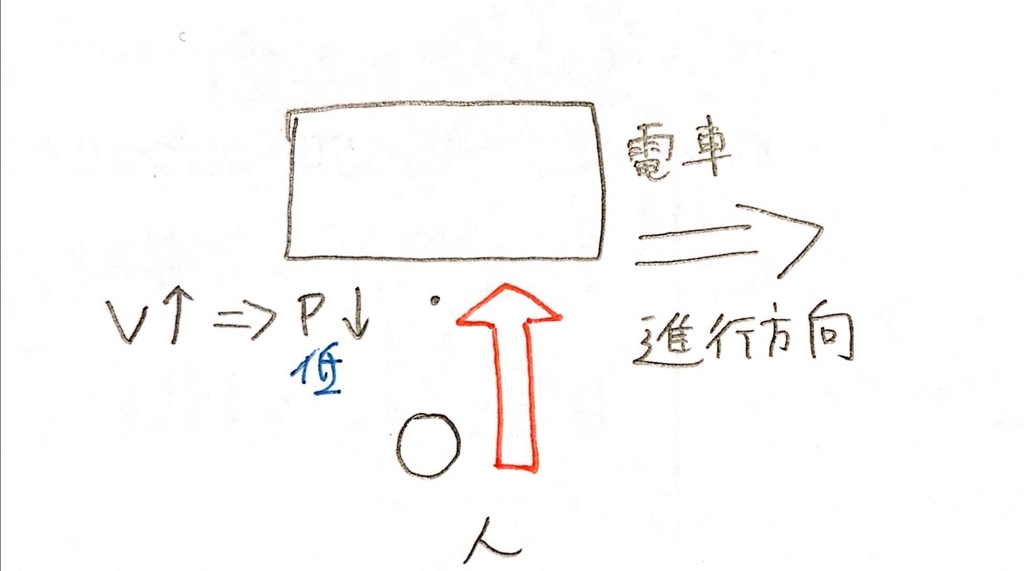
電車が通ると、電車の近くの空気はそれにつられて動きます。つまり速くなるわけです。するとベルヌーイの定理から、Vが大きくなるということは代わりにPが小さくなるということなので、電車付近の圧力Pが小さくなるってわけです。つまり僕たち人がいるところより、電車近くの圧力が小さくなります。そして電車の方に引き寄せられるように力が働くんです。
このベルヌーイの定理を簡単に体感できる実験があります。
みなさんお手元に紙を二枚用意して、向かい合わせにして持ってください。そしてその間に息をフーッと吹きかけると...
二枚がくっつくように引き寄せられます。これもベルヌーイの定理から理解できます。紙の間の空気が流れたことにより圧力が下がり、外から力が働いたわけですね。
こんな感じでベルヌーイの定理は身の回りに溢れています。
みなさんくれぐれも電車には近づかず、白線の内側まで下がってお待ちくださいね。